Just like many Go developers out there, I’m a big fan of Go standard library. Over the past few years I’ve been hacking on Go, I’ve discovered some real gems that not only made my life as a developer easier (no need to maintain unnecessary code), but they also made my code considerably more readable for others to follow. The last time I blogged I talked about how you can leverage Go standard library to generate weighted random draws.
Today I want to talk about a simple (i.e. not extremely efficient or optimised) implementation of the Breadth-first search (BFS) algorithm using just Go standard library along with some nifty tricks I’ve picked up over the past few years. I won’t discuss the BFS algorithm at length here. There is plenty of material available online. Intead, this post will show a practical implementation of BFS and demonstrate its correctness on a simple example. Let’s crack on!
Breadth-first search
BFS is a reasonably well known algorithm used for traversing or searching graphs. Among many other applications it’s used in Garbage Collectors for prutning the trees of no longer referenced memory or for finding the shortest path between two nodes in a graph. This post will describe how to use BFS to traverse all the nodes in graph.
This is handy in situation such as one I faced recently at my day job at Micro where I had to generate a topology of a local microservices network. As I’ll show here, the Go standard library makes this task quite easy.
Before we move on to discuss the algorithm, it’s worth pointing out that this post will describe the non-recursive variant of BFS. Usually, the most efficient graph traversing algorithms use recursion to walk the nodes of the graph, but for this particular task the non-recursive alternative is resonably efficient and performant, so we’ll stick with it.
The pseudocode for the non-recursive variant of BFS is pretty simple. But before we get to it, but before we spell it out it’s worth mentioning a few things.
Firstly, when traversing a graph, BFS splits the graph nodes into two groups:
- visited
- not [yet] visited
By doing this we skip the nodes which have already been visited, thus avoiding cycles leading to infinite loops.
Secondly, the algorithm uses FIFO queue for storing the graph nodes that have yet to be visited. Both of these points will hopefully become more clear as we walk through the actual implementation.
Let’s have a quick look at the BFS pseudocode now. It goes something like this:
- Initialize the queue for storing the nodes that have yet to be visited
- Pick any graph node and add it to the queue (NOTE: since this is a FIFO queue the node is pushed at the end of the queue)
- Take the first node from the front of the queue and add it to the list of visited nodes
- Add all adjacent nodes of the just visited node to the queue only if they haven’t already been visited
- Keep repeating 3 and 4 until the queue is empty
Let’s now walk through the actual implementation.
FIFO Queue
Implementing FIFO queue in Go is pretty straightforward if we decide to do the hard work ourselves. For the purpose of BFS we would need a data structure that will implement the following two methods:
Push(Node): pushes (enqueues) the node at the back of the queueFront(Node): dequeues the node from the front of the queue
One very naive way to implement this could look something like this:
package main
import "fmt"
// FIFO is a FIFO queue
type FIFO struct {
queue []interface{}
}
// New creates new FIFO and returns it
func New() *FIFO {
return &FIFO{
queue: make([]interface{}, 0),
}
}
// Push pushed node to the back of the queue
func (f *FIFO) Push(node interface{}) {
f.queue = append(f.queue, node)
}
// Front takes a value from the front of the queue and returns it
func (f *FIFO) Front() interface{} {
if len(f.queue) == 0 {
return nil
}
node := f.queue[0]
f.queue[0] = nil
f.queue = f.queue[1:]
return node
}
func main() {
vals := []int{1, 2, 3, 4}
fifo := New()
for _, val := range vals {
fifo.Push(val)
}
for {
front := fifo.Front()
if front == nil {
break
}
fmt.Println(front)
}
}
If you run the above program in Go playground, you’ll notice the values we push to the back of the queue are “popped” out from it in the same order they are pushed onto it just as we would expect from the FIFO queue:
$ go run main.go
1
2
3
4
Experienced Go programmers will notice a multitude of issues with this implementation (that’s why I called it naive right at the beginning). The most important issue is a major memory leak. If you are familiar with Go slice semantics you’d know that by appending to the internal queue slice (like we do in th Push method) we can potentially grow the program memory until we run out of it and the program crashes. In fact, that would have been a better case: we could potentially even crash the Operating System on which the program runs. Ooops!
Furthermore, even if we had infinite amount of memory, the performance of this implementation is horrenduously bad when used on large scale problems as Go append could be continuously allocating, reallocating and copying the memory here and there as nicely described here. Not good! On a more positive note, though, if we know the queue can not grow above some small threshold this implementation might do an OK job.
As I said at the beginning this post is about implementing BFS by taking advantage of the Go standard library. Unbeknownst (this must be the first time I’ve used this word!) to many, Go standard library has a little gem of a package which provides an efficient implemention of the queue we need: container/list. Actually, container/list implements a doubly linked list, but we can (ab)use it as a FIFO queue by only using its PushBack() and Front() methods which provide just enough functionality for what we need from FIFO queue! Few lines of code says a thousand words so here is a small code snippet that demonstrates this quite nicely:
package main
import (
"container/list"
"fmt"
)
func main() {
vals := []int{1, 2, 3, 4}
fifo := list.New()
for _, val := range vals {
fifo.PushBack(val)
}
for val := fifo.Front(); val != nil; val = val.Next() {
fmt.Println(val.Value)
}
}
Again, if you run this program in Go playground, you can verify the FIFO works as expected:
$ go run main.go
1
2
3
4
This is great: less code -> time saved -> much relief -> moving on!
BFS implementation
Now that we have the FIFO queue off our necks we can move on to the actual BFS implementation. Spoiler alert: the queue part may have been the most interesting part of this blog post, but bear with me if you are curious how this mystery works out!
Let’s define a simple graph data structure. This will by no means be the best way to model the problem, but it will serve us well in this blog post. Every graph has at least one node which can have some neighbours (or it can have none) – let’s call these neighbours “friends”. We can model a simple graph node as follows:
type node struct {
Id string
friends map[string]*node
}
NOTE: for simplicity we will use Go maps to track the node’s neighbours.
Let’s build a simple unidirected graph which has multiple nodes in it. Unidirected graphs can have cycles, and for this particular example we actually want the graph to have cycles so that we can demonstratethe the correctness of our BFS implementation when traversing the graph. We can build a 4 nodes graph like this:
node1 := &node{Id: "node1", friends: make(map[string]*node)}
node2 := &node{Id: "node2", friends: make(map[string]*node)}
node3 := &node{Id: "node3", friends: make(map[string]*node)}
// node2 is directly connected to node1
node2.friends[node1.Id] = node1
// node3 is directly connected to node2
node3.friends[node2.Id] = node2
// node1 is directly connected to node3
node1.friends[node3.Id] = node3
// root node; this graph is actually not a tree, but lets call this node root anyways
root := &node{Id: "root", friends: make(map[string]*node)}
graph := make(map[string]*node)
graph[root.Id] = root
graph[root.Id].friends[node1.Id] = node1
graph[root.Id].friends[node2.Id] = node2
graph[root.Id].friends[node3.Id] = node3
The graph we had so laboriously built above looks something like this:
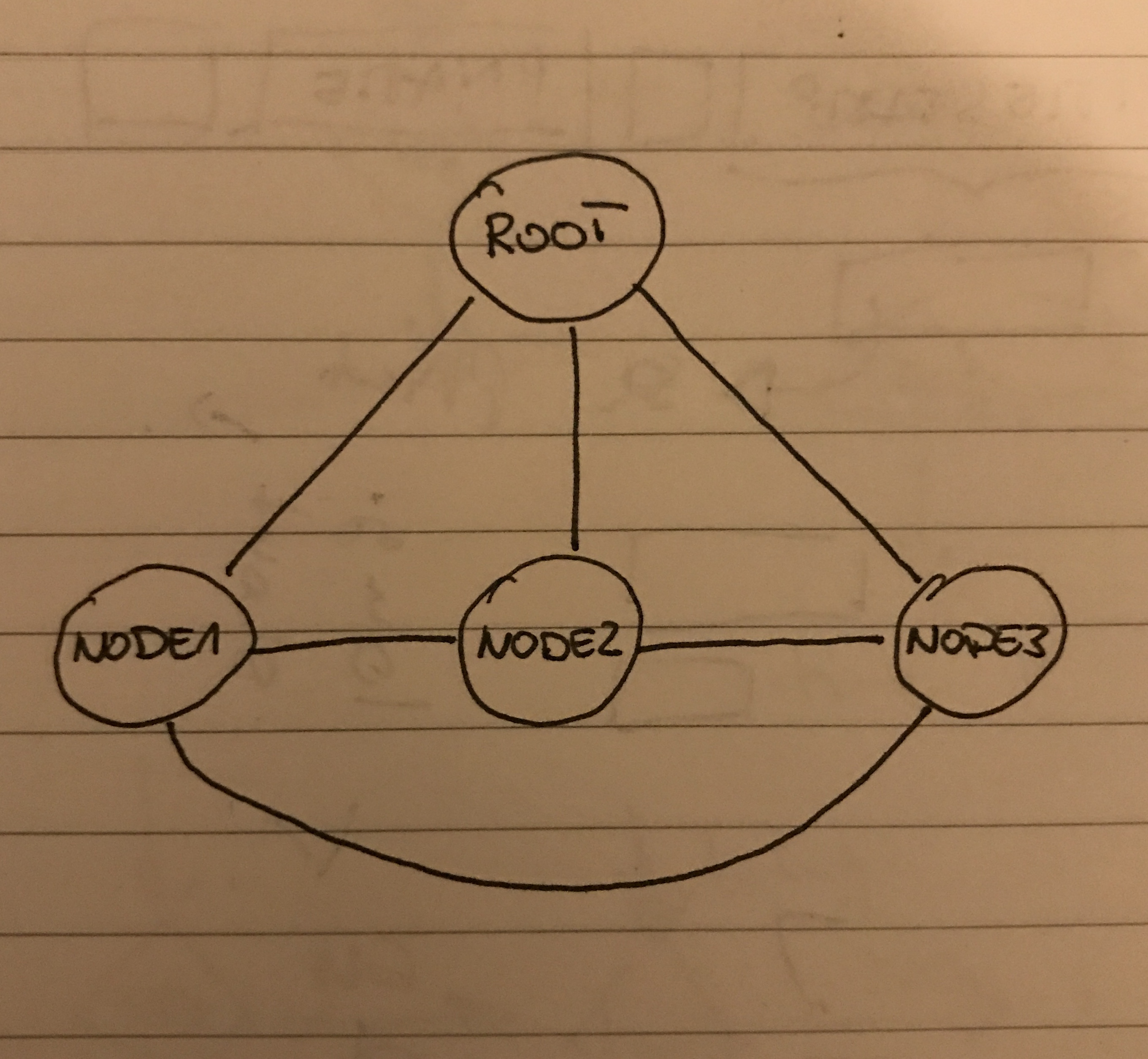
(Why, yes! That’s an image scribbled on my notepad taken by my phone)
Our goal now is to visit all the nodes in the graph (traverse the graph) and collect them into slice. Given the pseudocode of the BFS algorithm we had discussed earlier and taking the advantage of the container/list package we can write the whole algorithm in a few lines of code as follows:
//track the visited nodes
visited := make(map[string]*node)
// queue of the nodes to visit
queue := list.New()
queue.PushBack(node)
// add the root node to the map of the visited nodes
visited[node.Id] = node
for queue.Len() > 0 {
qnode := queue.Front()
// iterate through all of its friends
// mark the visited nodes; enqueue the non-visted
for id, node := range qnode.Value.(*node).friends {
if _, ok := visited[id]; !ok {
visited[id] = node
queue.PushBack(node)
}
}
queue.Remove(qnode)
}
That’s it! That’s the whole implementation! It only takes something about 15 lines of code (excluding the comments). Beautiful! Once the algorithm is finishes running the visited map will contain all the nodes in the graph. No less, no more!
We can easily verify the implementation works as expected by putting all the pieces together in a simple program:
package main
import (
"container/list"
"fmt"
)
// node is a graph node
type node struct {
Id string
friends map[string]*node
}
// Nodes returns a list of all graph nodes
func Nodes(n *node) []*node {
//track the visited nodes
visited := make(map[string]*node)
// queue of the nodes to visit
queue := list.New()
queue.PushBack(n)
// add the root node to the map of the visited nodes
visited[n.Id] = n
for queue.Len() > 0 {
qnode := queue.Front()
// iterate through all of its friends
// mark the visited nodes; enqueue the non-visted
for id, node := range qnode.Value.(*node).friends {
if _, ok := visited[id]; !ok {
visited[id] = node
queue.PushBack(node)
}
}
queue.Remove(qnode)
}
nodes := make([]*node, 0)
// collecte all the nodes into slice
for _, node := range visited {
nodes = append(nodes, node)
}
return nodes
}
func main() {
node1 := &node{Id: "node1", friends: make(map[string]*node)}
node2 := &node{Id: "node2", friends: make(map[string]*node)}
node3 := &node{Id: "node3", friends: make(map[string]*node)}
// node2 is directly connected to node1
node2.friends[node1.Id] = node1
// node3 is directly connected to node2
node3.friends[node2.Id] = node2
// node1 is directly connected to node3
node1.friends[node3.Id] = node3
// root node; this graph is actually not a tree so it does not have a root node
root := &node{Id: "root", friends: make(map[string]*node)}
n := make(map[string]*node)
n[root.Id] = root
n[root.Id].friends[node1.Id] = node1
n[root.Id].friends[node2.Id] = node2
n[root.Id].friends[node3.Id] = node3
nodes := Nodes(root)
for _, node := range nodes {
fmt.Printf("%+v\n", node.Id)
}
}
By running the above program in Go playground we can verify it has correctly collected all the nodes present in the graph.
Conclusion
This blog post has once again demonstrated the power of Go standard library. We’ve walked from a simple and inefficient implementation of FIFO queue, to the one which took advantage of the features provided by container/list package. We’ve then used it in the full BFS implementation in only on a few lines of Go code. Magic!
By taking advantage of the wealthe of packages provided by Go standard library we can save ourselves a lot of time that can easily be sunk into maintaining unnecessary source code and focus on the more important things in our business logic. One another advantage of using just Go standard library is we can easily share the fully executable programs by sharing Go playground links since we do not need any external dependencies. This can be a major win when colaboratin on debugging program behaviour.
Keep on hacking, Gopher friends! Until next time!